Cianobacterias, heterocistes, Turing... Vamos a ver: ¿de qué demonios va esto y sobre todo, por qué me interesa toda esta peña? Pues por mucho más de lo que usted se cree, escéptico lector. Para empezar, las cianobacterias (en la foto) son muy importantes para producirbiocarburante, pero para qué le voy a engañar, eso francamente a mí me importa poco. Lo que me gusta es que las cianobacterias, además de ser muy valiosas proveyéndonos de oxígenoy de nitrógeno, son un laboratorio viviente, que nos permite empezar a vislumbrar como funciona el proceso de diferenciación celular, por el que hemos llegado usted y yo a tener unhígado y un cerebro y un corazón y demás ascos internos que nos mantienen vivos. Toda la maquinaria de expresión genética es un proceso muy complicado que, al contrario de lo que se creía cuando se llevó a cabo el proyecto Genoma Humano, va mucho más allá de saber qué gen hace qué. Nos adentramos así en el terreno de la epigenética, en el más amplio de la regulación genética y en la interacción de esta con el crecimiento de los organismos. El trabajo que le voy a resumir contribuye a entreabrir la puerta que nos aclare estas cosas. Así que sí, amigo lector, le interesan las cianobacterias, aunque usted no lo sepa. Lea, lea.
Las cianobacterias son, como su propio nombre indica, bacterias, cuya principal característica es que son capaces de hacer la fotosíntesis y, por tanto, de producir oxígeno, y por eso son una gente fundamental para la vida en la Tierra. De hecho, amigo lector, puede que haya oído hablar de ellas bajo el nombre "algas azules" y de que son una importante contribución al oxígeno terrestre y, sobre todo, marino. Pero no son algas, dado que soncélulas procariotas ("sin núcleo"), a diferencia de las algas o de usted mismo, formado porcélulas eucariotas ("con núcleo"), por lo que hace tiempo se prefiere el nombre de cianobacteria. En todo caso, son importantes, además de porque producen oxígeno, porque fijan nitrógeno de la atmósfera (y, por si no lo sabe, el nitrógeno es igual de imprescindible para la vida, se necesita para las proteínas y los ácidos nucleicos, como el ADN; sólo bacterias y arqueas pueden hacer esto) y porque son un poco como organismos multicelulares primitivos. Y desde hace unos días, además, porque sabemos que entender su estructura filamentosa requiere ir más allá de la matemática de Turing.
Como muestra la foto superior, nuestras amigas las cianobacterias gustan de vivir en filamentos, en los que cada una está pegada a otras dos, una a cada lado (excepto, obviamente, las de los extremos). Organizadas en esa estructura, van haciendo sus cosas de cianobacterias, reproduciéndose por duplicación, y haciendo que el filamento crezca. Hasta aquí, una vida bastante monótona y no muy interesante. Sin embargo, cuando pintan bastosen el tema del nitrógeno, porque escasee por el motivo que sea, se produce un fenómeno de diferenciación celular (que es lo que pasa cuando un óvulo fecundado, con una sóla célula, da lugar a un bicho o una planta): una de cada diez (más o menos) cianobacterias se convierten en heterocistes: su pared celular se vuelve más gruesa y se convierten en una fábrica de generar nitrógeno para aprovisionar al resto de cianobacterias (nota pedante: esto no les pasa a todos los tipos de cianobacterias, pero sí a una mayoría, así que aceptémoslo sin más explicaciones engorrosas). ¿Y por qué no se busca la vida cada cianobacteria y se genera su propio nitrógeno? Pues, fundamentalmente, porque la maquinaria química necesaria para fijar nitrógeno se destruye muy fácilmente en presencia de oxígeno. Así que mientras el resto de cianobacterias en el filamento hace la fotosíntesis, los heterocistes fijan el nitrógeno que necesitan todas, recibiendo a su vez nutrientes de sus vecinas. ¡Toma división del trabajo bacteriana!
Pero he dicho antes que esto iba de patrones, y aquí viene a cuento el "una de cada diez" del párrafo anterior. Cuando comienza el proceso de formación de heterocistes, no tiene lugar al azar, sino que a lo largo del filamento hay una distancia de aproximadamente diez células normales entre heterocistes. Lo que pasa es que estas células normales siguen reproduciéndose, mientras que los heterocistes pierden la capacidad de duplicarse. Lógicamente, con el tiempo, a medida que las bacterias que hay entre medias se duplican, la distancia entre heterocistes, medida en número de células, aumenta. Es entonces cuando algo ocurre y alguna de esas células entre medias se convierte en hetorociste, y vuelta a empezar. Es decir, aparece un patrón espacial auto-organizado y además sostenido en el tiempo, cuyo origen no se entendía gran cosa... hasta ahora, que Javier Muñoz-García y Saúl Ares (brillantes científicos del grupo al que pertenezco, el GISC, y que como no los estabilicemos acabarán marchándose, claro) han propuesto un modelo matemático que lo explica con bastante precisión, en un trabajo publicado en PNAS.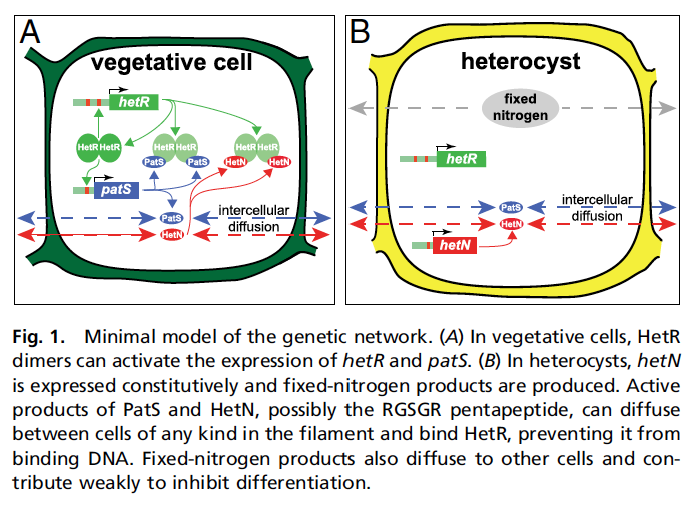
El modelo que proponen Muñoz-García y Ares se basa en el juego entre la expresión de tres genes, hetR, hetN, y patS. Los dos primeros se expresan sobre todo en los heterocistes, mientras que hetR y patS lo hacen en las células normales (llamadas habitualmente vegetativas). Además, las proteínas a las que dan lugar dichos genes (que se denotan con el nombre del gen pero en letra ordinaria, recta) se pueden difundir y pasar de una célula a otra. Estas proteínas afectan a su vez la expresión de los genes... Un pequeño lío, ¿no? Vamos a ver si lo puedo explicar en breve:
- El gen hetR está íntimamente ligado al proceso de formación del heterociste, como se ha visto en investigaciones anteriores, y se expresa cuando falta nitrógeno.
- La proteína HetR forma dímeros (dos moléculas enlazadas) que al unirse al ADN hacen que se siga expresando el gen hetR pero también el patS.
- patS produce un compuesto que se liga a la proteína HetR e impide que se enlace al ADN, con lo cual ya no puede contribuir a que se expresen los genes. Por cierto, la proteína HetN tiene el mismo compuesto y el mismo efecto.
- La proteína PatS sólo se produce en las células vegetativas; a su vez, HetN sólo se produce en los heterocistes.
- Finalmente, las células en las que el nivel de proteína HetR supera un cierto umbral durante un cierto tiempo, se transforman en heterocistes.
Para el lector más aficionado a una visión abstracta, lo que hay aquí son tres mecanismos básicos: autoactivación local (hetR produce HetR que a su vez induce más producción de HetR), inhibición a distancia en fases tempranas (debida a la difusión de PatS) e inhibición a distancia tardía (debida a la difusión de HetN, cuya producción se activa más tarde que la de PatS).
Ahora se cogen todos estos ingredientes, se añade la duplicación de las células normales, que ocurre con una periodicidad bastante precisa (pero no perfecta), se añade algo de ruido en las variables del modelo (básicamente, las concentraciones de los distintos productos químicos en los distintos sitios) y se lleva todo el guiso a un programa de ordenador. Un ejemplo del resultado de las simulaciones es la siguiente figura:
En ella apreciamos la aparición de heterocistes, rodeados por su membrana amarilla, mientras que el color verde representa la concentración de HetR. Se ve cómo se reproduce el patrón en el que se van formando los heterocistes y que la distancia es más o menos la misma que la que se observa experimentalmente. De todas maneras, este es uno de esos casos en los que una imagen no vale más que mil palabras, sino que lo que hace falta son videos, y gracias a los autores del trabajo los tenemos disponibles en esta página. Si uno recorre la serie de cinco vídeos, comprueba que todos los ingredientes del modelo son necesarios, porque cuando alguno falla, las cosas no funcionan: se forman demasiados heterocistes, o están juntos, o faltan productos derivados del fijado del nitrógeno, o cualquier otra calamidad (nota pedante 2: para que el modelo funcione fetén hay que poner un segundo inhibidor tardío que tiene que ver con estos productos; no es que cambie mucho las cosas, y no las cambia cualitativamente, pero para que los números cuadren en algunos casos, como falta de HetN, sí que hay que considerar este mecanismo adicional). Además, y aunque yo no soy muy partidario de los videos, aconsejo verlos en este caso, porque así uno se da cuenta de lo difícil del problema porque es realmente dinámico: una cosa importante es observar, por ejemplo, que el patrón de un heterociste cada diez células normales aparece sólo, de manera auto-organizada como decía antes, sin necesidad de imponer eso desde el principio iniciando el patrón "a mano" en algunas células. Es una longitud característica que aparece espontáneamente y como producto de la interacción entre la producción de HetR y la producción y difusión de PatS.
Y volviendo ahora a mi afirmación inicial, ¿por qué este modelo va más allá de la propuesta pionera de Turing? (Observe que desde el título nos habíamos olvidado de Alan Turing, del que ya hablé en NeG, concretamente de su faceta de pionero de la biología matemática, fascinado por entender los patrones que aparecen en la naturaleza.) Pues por varias razones, unas más técnicas que otras, pero la principal es que el activador de la diferenciación de los heterocistes, HetR, no se difunde, mientras que la dinámica de Turing contempla esencialmente dos sustancias, una que activa y otra que inhibe, que se difunden. Como consecuencia de este hecho, el modelo de Muñoz-García y Ares es muy importante en tanto en cuanto es robusto: cambios de los parámetros de la simulación en un rango razonable no alteran el resultado. Se siguen formando los heterocistes a la distancia correcta, en el tiempo correcto, sin grandes variaciones, y sólo se forma ese patrón, independientemente de cómo se inicialice la simulación. En el caso de Turing, por el contrario, las longitudes típicas de los parámetros son muy sensibles, por ejemplo, a las difusividades de los compuestos que intervienen, y es muy normal que para los mismos parámetros se pueda formar uno u otro patrón simplemente por azar (nota pedante 3: aquí convendría citar al recientemente fallecido Hans Meinhardt, que fue realmente quién consideró distintas longitudes de difusión para los reactivos, pero no me puedo extender sobre el tema). Así pues, la propuesta de este modelo, que involucra dos inhibidores, y que es capaz de estabilizar un patrón en un sistema que crece rápidamente, es un paso importante para la propia matemática de los procesos de reacción-difusión. Con razón decía J. E. Cohen que "la matemática es el próximo microscopio de la biología, sólo que mejor, y la biología es la próxima física de las matemáticas, sólo que mejor." Como se suele decir, ¡seguiremos informando!
Si (
No(